Batch 3 - Class 173 - McNugget Numbers

• [Part of lesson plan below]

• You have two kinds of packets of chocolates - ones that have 5 chocolates in them, and ones that have 7 chocolates in them. What is the largest number of chocolates you can't give away, assuming you can't open the packets to do so
• Let kids work with smaller numbers
• Introduce the idea of "relatively prime" - what does that mean. What will happen if we divide successive multiples of the larger number by the smaller number? If we start to fill the number line with multiples of smaller number, then the larger number (seen as multiple of smaller number plus a remainder, and so on) - how many multiples of larger number will cover all the "modulos"? Hence what should the largest non-attainable number look like?
• For example, all numbers are either 5x or (5x+1) or (5x+2) or (5x+3) or (5x+4). Now 7 covers all numbers of (5x+2) kind, 7x2 covers (5x+4), 7x3 covers (5x+1), 7x4 covers (5x+3). So the largest number should be 7x4 minus the last number of the nature 5x+3, which is same as 7x4-5, which is 7x5-7-5
• Answer: 23 (This is called the Frobenius number of (5,7))
• Let kids work through the problems of larger size
• What happens when the numbers are not relatively prime - example 6 and 8
• Then such largest number is infinite - this is because all modulos of the smaller number are not covered.
•  McNugget numbers - McDonald's Chicken McNuggets (prior to introduction of happy meals) was 6, 9 and 20. What is the largest non-McNugget number (i.e. a number that can't be formed by integral combination of the three boxes)
• Note that if you can form 6 consecutive numbers, then everything beyond that is possible, but just adding more 6-boxes to those numbers
• Can you use the two number solution above to guide you in finding the three number solution here?
• Now there is a 4 box in "Happy Meal" - what is the largest non-McNugget number now?
• Answer: 11
• In some countries, the 9 box is replaced by a 10 box - what is the largest non-McNugget number now?
• Answer: Infinite, since any odd number can not be made
• Ninety-four bricks, each measuring 4"x10"x19" are stacked one on top of another to form a tower 94 bricks tall. Each brick can be oriented so that it contributes 4" or 10" or 19" to the total height of the tower. How many different tower heights can be achieved using all the ninety four bricks?
• Kids may try a smaller problem - like number of towere heights with 10 bricks of height 4, 6 and 7
• Answer: 465. The minimum height of such a tower is 94x4, and then we can start to measure the increment by realigning each brick. These increments can be 0, 6 or 15 - since these are divisible by 3, its same as increments of 0, 2 or 5. At the lower end, using increments of 2 and 5, we can form all combinations except 1 and 3. But there is also some numbers we can't form at the upper end because of limitations on number of bricks. These can be found by considering total height of 94x19 and considerating decrements of 15, 9 and 0 - equivalent of 5 and 3. These lead to all decrements except 1, 2, 4, 7. So total heights possible are numbers from 0 to 94x5, except 6 numbers. Hence the answer is 465

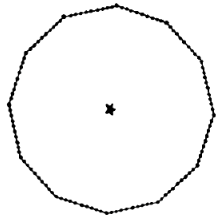
• (536Dudeney - 266) An officer wished to form his men into 12 rows, with 11 men in each row, so that he could place himself at a point that would be equidistant from every row. However, there were only 120 men. Was it possible to carry out the order?
• Answer: The men may be arranged along rows as shown, with the officer at the center